我们对一个算法进行评价,一般有 2 个重要依据:时间复杂度 与 空间复杂度。
# 1.1 时间复杂度
| 名称 | 运行时间 T(n) | 时间举例 | 算法举例 |
|---|---|---|---|
| 常数 | O(1) | 3 | - |
| 线性 | O(n) | n | 遍历数组 |
| 平方 | O(n^2) | n^2 | 冒泡排序 |
| 对数 | O(log(n)) | log(n) | 二分查找 |
| 指数 | O(2^n) | 2^n | 斐波那契数列 |
- O(1)
算法所执行的时间不会随着 n 的大小变化,不管 n 是什么,我们都称为 O(1)。
const a = 1
- O(n)
下面的 for 循环,会执行 n 次,不管 n 是几,都称做 O(n)。
for (let i = 0; i < n; i++) {}
- O(n2)
2 层嵌套循环,内层循环会执行 n*n 次;也就是 n^2,随着 n 的增大,复杂度会随着 n 的增大,复杂度会随着平方级增加。
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; i++) {}
}
2
3
- O(log(n)) 对数复杂度
高中数学知识, y = loga x 叫做对数函数,a 是对数;y 就是以 a 为底 x 的对数。
如果,即 a 的 x 次方等于 N(a > 0,且 a ≠ 1),那么数 x 叫做以 a 为底 N 的对数(logarithm),其中,a 叫做对数的底数,N 叫做真数,x 叫做 “以 a 为底 N 的对数”。
for (leti = 1; i <= n; i *= 2) {
console.log(i)
}
2
3
我们可以看出,这个算法对元素进行跳跃式输出;就是数组从下标开始,每次都会乘以 2,直到 i 小于 n 的时候结束循环。
1*2 -> 2*2 -> 4*2 -> 8*2 ....
2^1 -> 2^2 -> 2^3 -> 2^4 ....
假设 i 在 i = i*2 的规则递增了 x 次之后,i <= n 开始不成立;那么我们可以推算出下面一个数学方程式:
2 ^ (x >= n)
x 解出来,就是大于等于以 2 为底 n 的对数。
x>= log2 n
只有当 x>= log2 n 循环才成立;才会执行循环体。
如果把上面的 i*= 2 改为 i*= 3,那么这段代码的时间复杂度就是 log3 n 。
注意涉及到对数的时间复杂度,底数和系数都是要被简化掉的。那么这里的 O(n) 就可以表示为:
O(log(n))
- O(2^n)
我们常见的斐波那契数列,F (0) = 1,F (2) = 1, F (n) = F (n − 1) + F (n − 2);时间复杂度该如何考虑?
function fibonacci(n){
if (n === 0 || n === 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
2
3
4
5
6
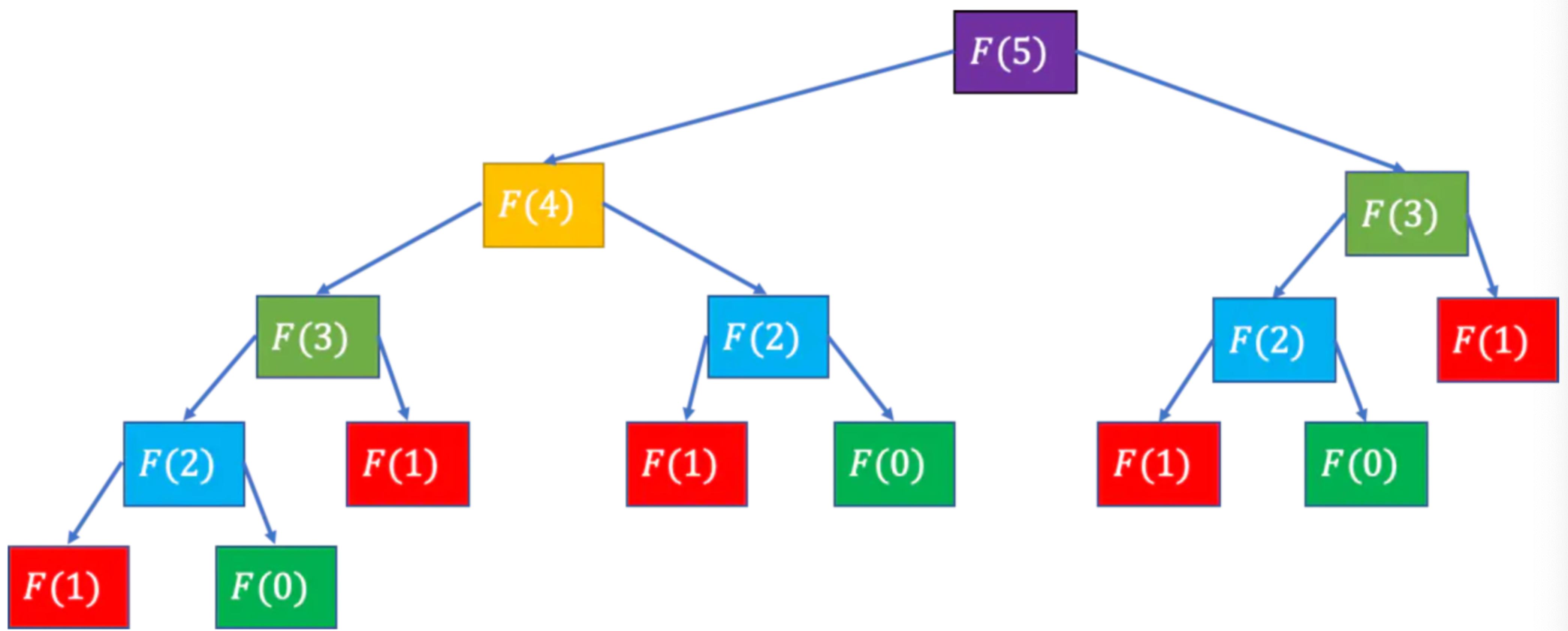
假如 n=5,那么递归的的时间复杂度该怎么算?
在 n 层的完全二叉树中,节点的总数为 2n − 1 ,所以得到 F(n) 中递归数目的上限为 2n − 1 。因此我们可以大概估出 F(n) 的时间复杂度为 O(2^n)。在斐波那契中有大量重复的计算,我们可以把已经计算过的存起来,同样的计算再取出来。
# 1.2 空间复杂度
空间复杂度是对算法运行过程中临时占用空间大小的度量,一个算法所需的存储空间用 f (n) 表 示,可得出 S(n) = O(f(n)) ,其中 n 为问题的规模,S(n) 表示空间复杂度。通常用 S(n) 来定义。
常见的空间复杂度有 O(1)、O(n) 和 O(n^2)。
- O(1)
const a = 1
const b = 1
console.log(a)
2
3
上面占用空间的变量:a、b;分配的空间不会随着处理数据变化而变化,因此得到的空间复杂度为 O(1)。
let arr = [1, 2, 3, 4]
let len = arr.length
for (var i = 0; i < len; i++) {
console.log(arr[i])
}
2
3
4
5
上面占用空间的变量:arr、len、i;做了多次循环,都是时间上的开销,在执行循环体时,并没有开辟新的空间;因此占用的内存是固定的,它的空间复杂度为 O(1)。
- O(n)
let arr = []
for (let i = 0; i < n; i++) {
arr[i] = i
}
2
3
4
上面占用空间的变量:arr、i 、n;可以看出 arr 并不是一个一成不变的数组,arr 随 n 决定,会随着 n 的增大而增大,所以这个算法的空间复杂 O(n);所以它是线性的。
- O(n^2)
let arr = []
for (let i = 0; i < n; i++) {
arr[i] = []
for (let j = 0; j < n; j++) {
arr[i][j] = i + j
}
}
2
3
4
5
6
7
上面占用空间的变量:arr、i 、n;可以看出 arr 并不是一个一成不变的数组,内层循环会执行 n*n 次,因此空间复杂度为 O(n^2)。
# 1.3 总结
# 时间空间相互转换
对于一个算法来说,它的时间复杂度和空间复杂度往往是相互影响的。 那我们熟悉的 Chrome 来说,流畅性方面比其他厂商好了多人,但是占用的内存空间略大。 当追求一个较好的时间复杂度时,可能需要消耗更多的储存空间。 反之,如果追求较好的空间复杂 度,算法执行的时间可能就会变长。
常见的复杂度不多,从低到高排列就这么几个: O(1) 、 O(log(n)) 、 O(n) 、 O(n^2) 、O(2^n)。
数据结构 →

